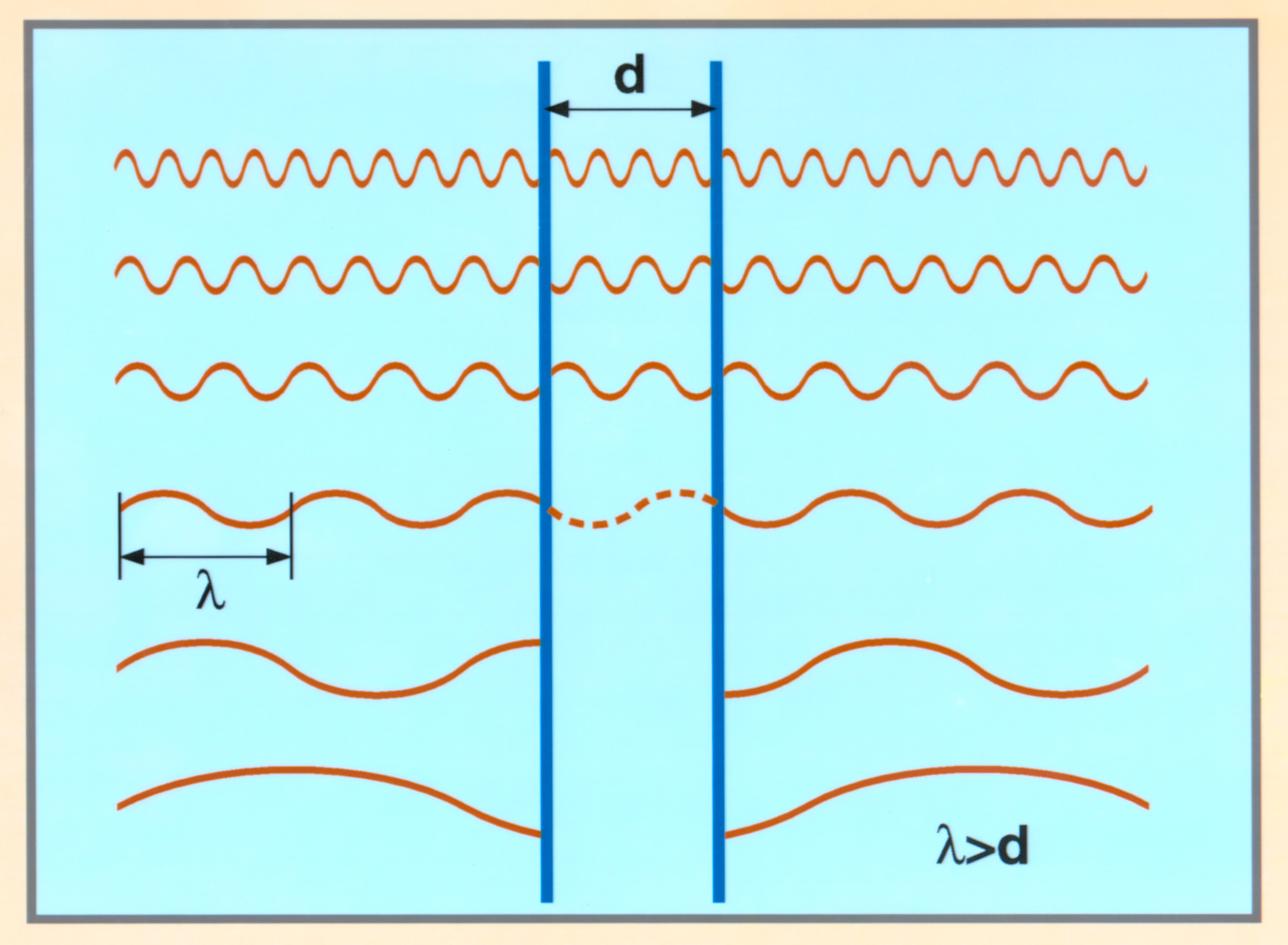
The Casimir force between parallel conducting plates is a real, macroscopic effect. It has now been measured to a precision of about one percent and is beginning to be developed as a source of mechanical action in microelectromechanical systems (MEMS) devices (see "Force from empty space drives a machine" in the Feb. 10, 2001 Science News). The force is due to the virtual particles and electromagnetic fluctuations that constitute the quantum vacuum. However the force can be very easily calculated by assuming that there is a real underlying sea of zero-point energy in the form of a zero-point field, and that certain modes of the field (shown for illustrative purposes on the left as simple standing waves) are excluded in the region between the (blue) plates (see "Radiation pressure from the vacuum: Physical interpretation of the Casimir force," Milonni, Cook & Goggin, Phys. Rev. A, 38, 1621, 1988; also "Repulsive Casimir force as a result of vacuum radiation pressure," Hushwater, Amer. J. Phys., 65, 381, 1997). Thus irrespective of the real vs. virtual ontology of the zero-point field, calculations assuming it to be real result in the accurate prediction of a very real force. Our approach to inertia is similar. If we represent the electromagnetic quantum vacuum as a real zero-point field and use the techniques of stochastic electrodynamics, we predict the existence of a zero-point energy flow in accelerated reference frames which we call the Rindler flux. Now physically, the Rindler flux must consist of virtual photons. Yet if we allow this virtual flow of energy to interact with matter in a manner analogous to the Casimir force interaction, we also arrive at a force: a reaction force that has the "proportional to acceleration" characteristic that might account for the origin of inertia.

VISUALIZING THE ORIGIN OF THE RINDLER FLUX

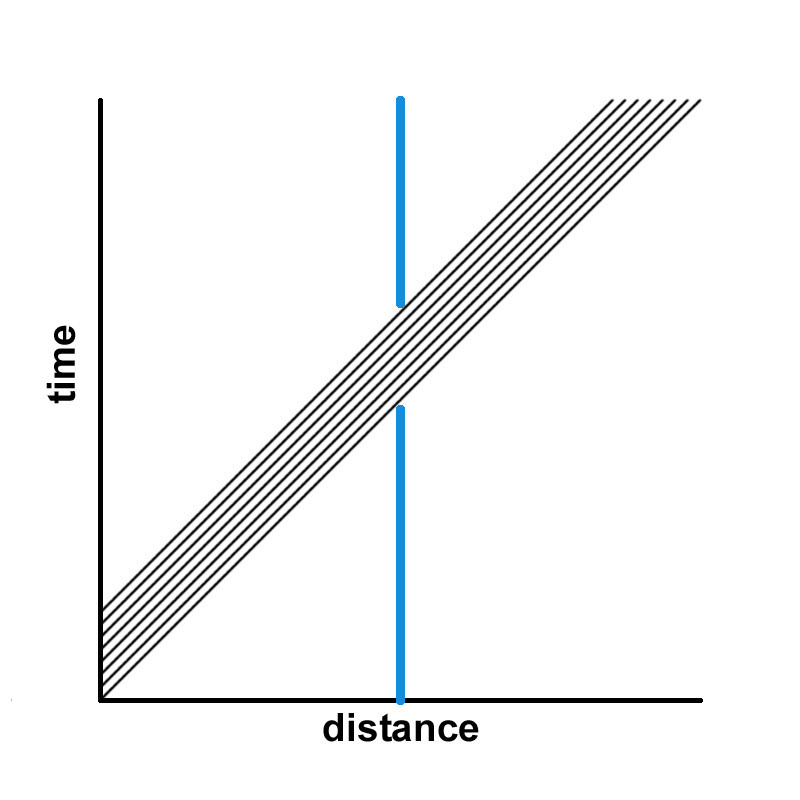
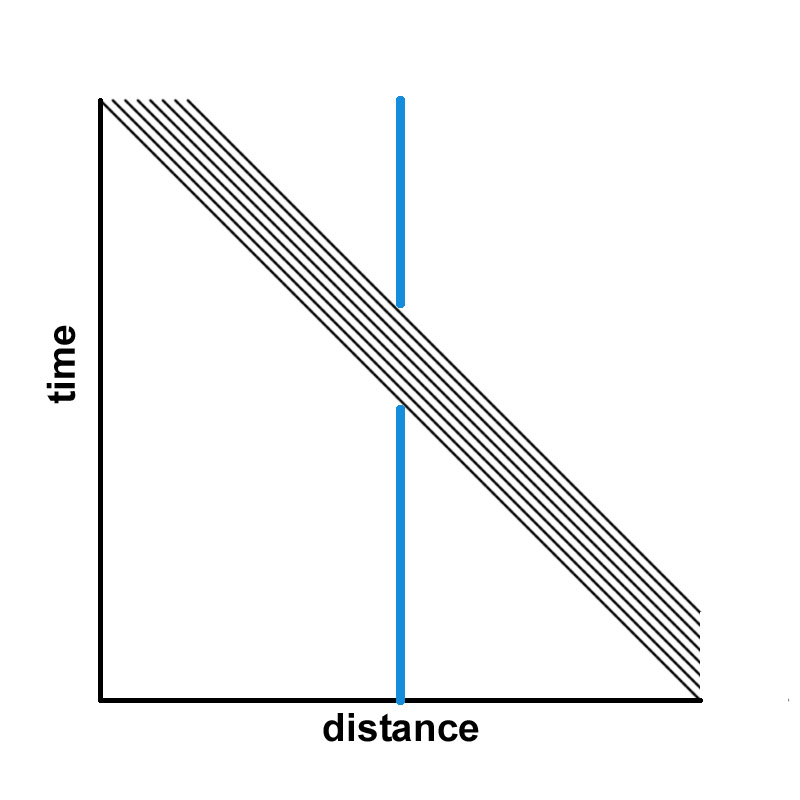
Stochastic electrodynamics models the electromagnetic quantum vacuum in the approximation that it may be represented by propagating plane waves of electromagnetic radiation, usually called the zero-point field. In a customary spacetime diagram, electromagnetic radiation (light) propagation is represented by lines at 45 degree angles. We wish to show pictorially the origin of a Rindler flux of quantum vacuum radiation by examining the flow of electromagnetic radiation which a detector will measure in three different cases.

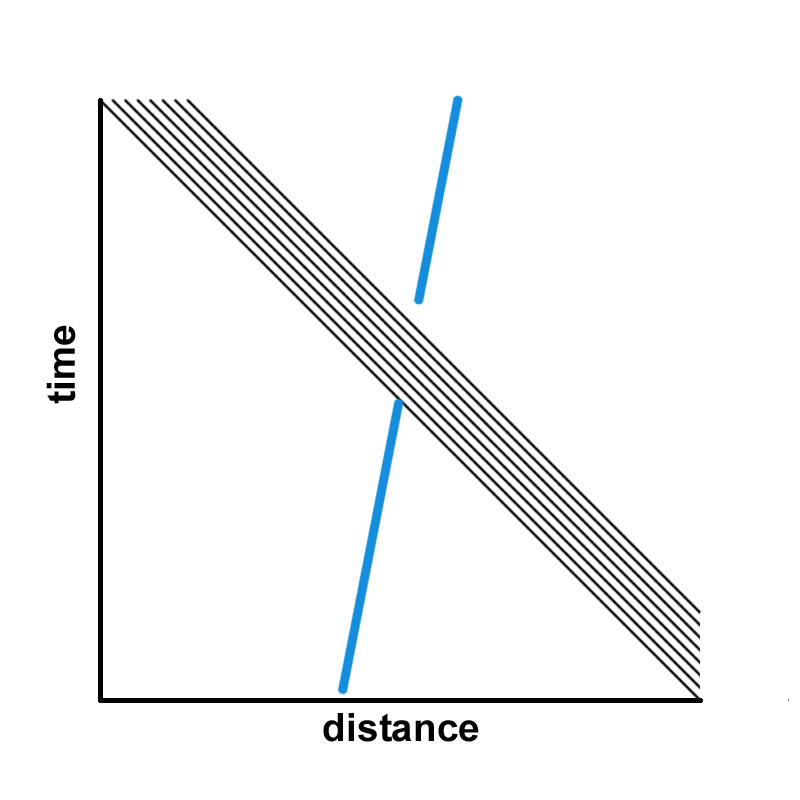
CASE 1: DETECTOR STATIONARY IN LAB FRAME -- The blue worldline in each figure represents a detector with a shutter. It is fixed in place but advancing in time, with time increasing from the bottom to the top. At a given moment in time, the shutter opens and admits a certain amount of radiation. It then closes again. In the left-hand diagram, light is propagating from left to right, i.e. in the +x direction. In the right-hand diagram, light is propagating from right to left., i.e. in the -x direction. Clearly in both cases the same amount of radiation will enter during the open-shutter interval.

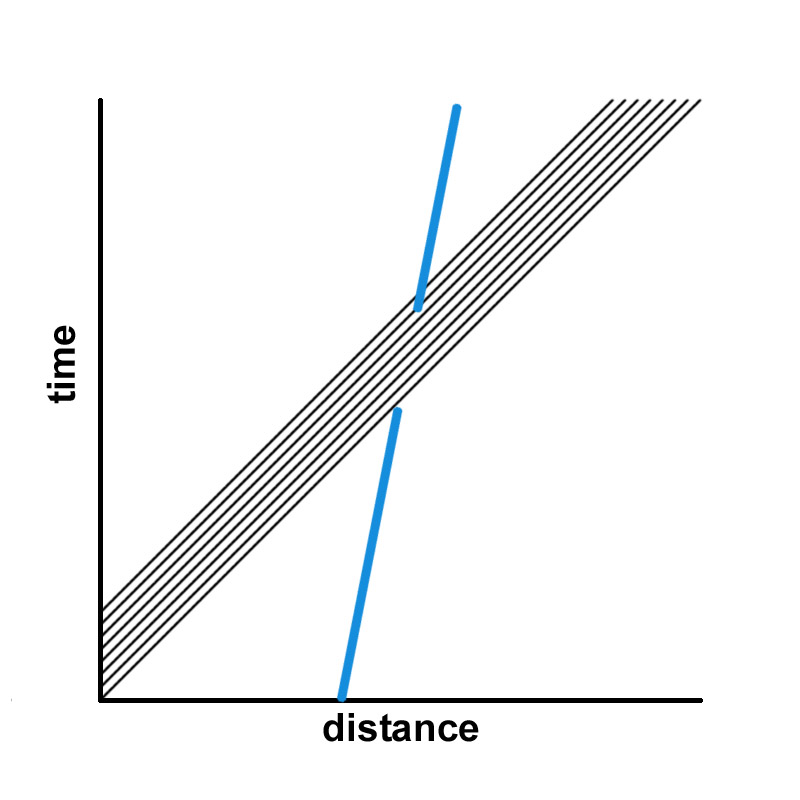
CASE 2: DETECTOR IN CONSTANT MOTION WITH RESPECT TO LAB FRAME -- We now have a situation in which the detector is in motion with respect to our laboratory frame. The blue worldline of the detector is therefore at an angle since its x-coordinate increases as time advances. The time interval of the shutter opening is the same as in case 1. But clearly now there is an asymmetry from the perspective of the lab frame. Some of the radiation from the left will not be detected because the shutter closes too soon. On the other hand the shutter stays open beyond the last depicted light ray from the right. More radiation (not shown) can continue to flow in from that direction before the shutter closes. In the frame of the detector, of course, there is no asymmetry. The detector judges itself to be case 1.

The situation is analogous to time dilation in special relativity. If I am in rapid enough motion with respect to an observer, that observer will notice that my clock appears to be moving more slowly than his. But my clock looks fine to me. In fact, I see the observer's clock running slowly. So the bottom line is that the lab frame observer would expect there to be a net flow of energy through the detector, but the detector would see no such flow.

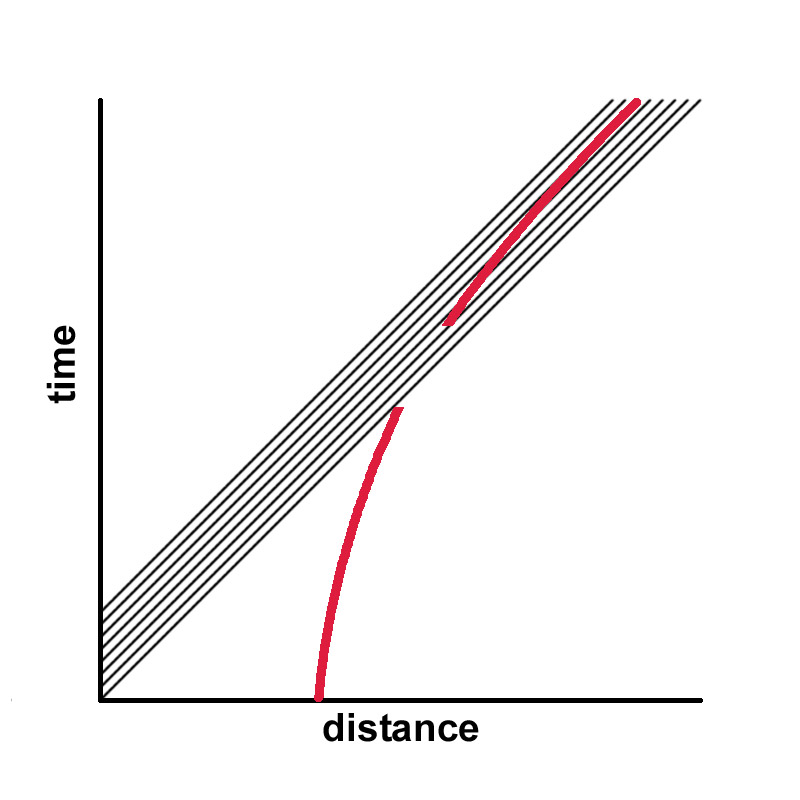
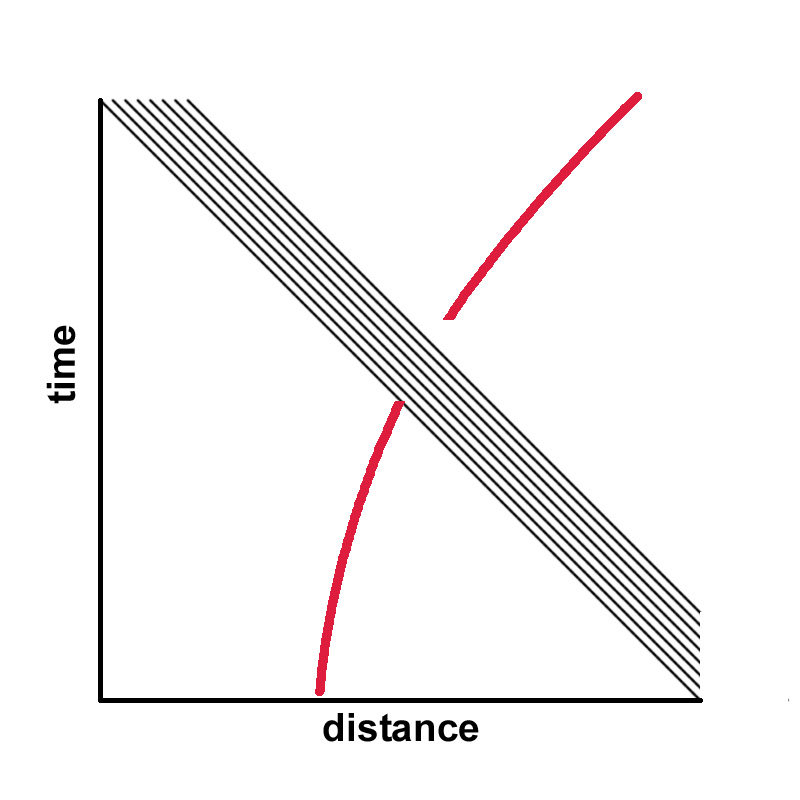
CASE 3: DETECTOR UNDERGOING CONSTANT ACCELERATION -- No Rindler flux is ever experienced by a detector in case 2 because the detector is always at rest with respect to itself. Moreover the strength of the Rindler flux in case 2 depends entirely on the relative motion of the detector and the lab frame, which can be take on any value. The case of acceleration is more subtle and involves more than just one instantaneous reference frame. When accelerating, an object continuously changes references frames, and this does lead to an effect since dynamics necessarily involves time-dependent processes over some time interval dt. When accelerating, the detector continually undergoes a change of reference frame with respect to its own previous reference frame. Each moment of time that the detector experiences is connected to a previous moment in time in which it was in a slightly different reference frame. This change of frame is no longer arbitrary, but in fact depends on the curvature of the worldline, which is hyperbolic for the case of constant acceleration. What we have shown (Rueda and Haisch 1998a, 1998b) is that this minute change in the energy flux results in a reaction force that acts upon the detector with the "proportional to acceleration" characteristic that might account for the origin of inertia.

There is a connection as well to an event horizon. As shown, the hyperbolic worldline of the constantly-accelerating detector asymptotically approaches, but never reaches, the topmost lightcone in the left-hand diagram. Nothing to the left of that lightcone can have any influence on the accelerating detector. The relationship of an event horizon in this case to the black hole event horizon responsible for Unruh-Davies radiation needs further elucidation.

CASIMIR FORCE
Depending on where in frequency one chooses to cut off the zero-point field in the SED representation, the total energy density, call it E, is enormous. This energy density is arguably improperly defined (due to the unknown cutoff) and not physically real, yet in spite of that one can calculate a very precisely defined difference in energy density inside a Casmir cavity vs. in free space, E(free space)-E(in cavity), and this tiny difference very accurately translates into a radiation pressure which can account for the Casimir force.

INERTIA REACTION FORCE
In an infinitesimal time interval dt an accelerating object will move from one coordinate frame into another. The Rindler flux in each frame is arguably improperly defined and not physically real, yet one can show that there does exist a very well defined difference in that flux as perceived by an accelerating detector in any infinitesimal time interval dt. That difference proves to be proportional to acceleration and hence can be associated with a resulting reaction force which acts like inertia.

(RF figures by Marsha Sims)